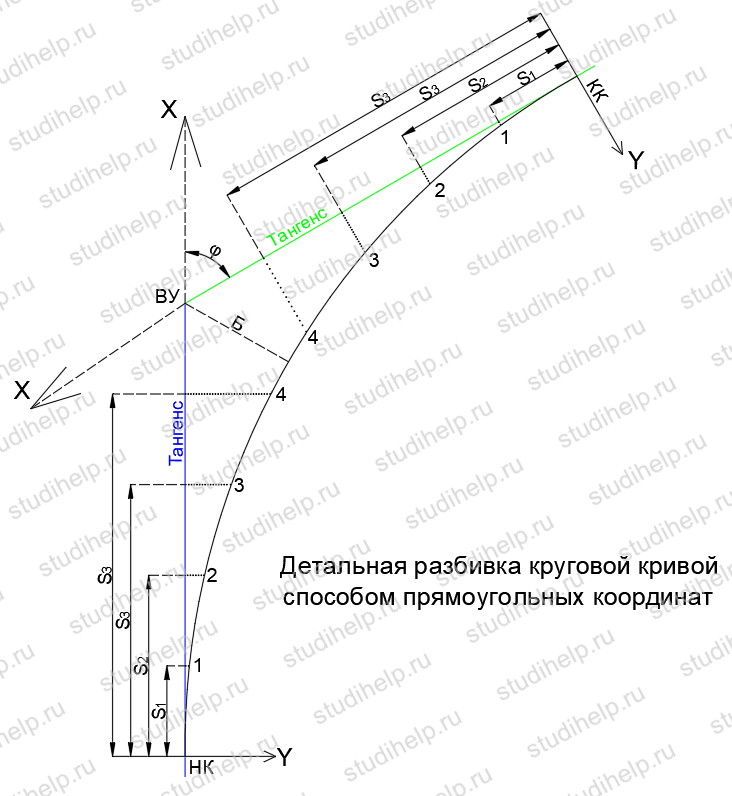
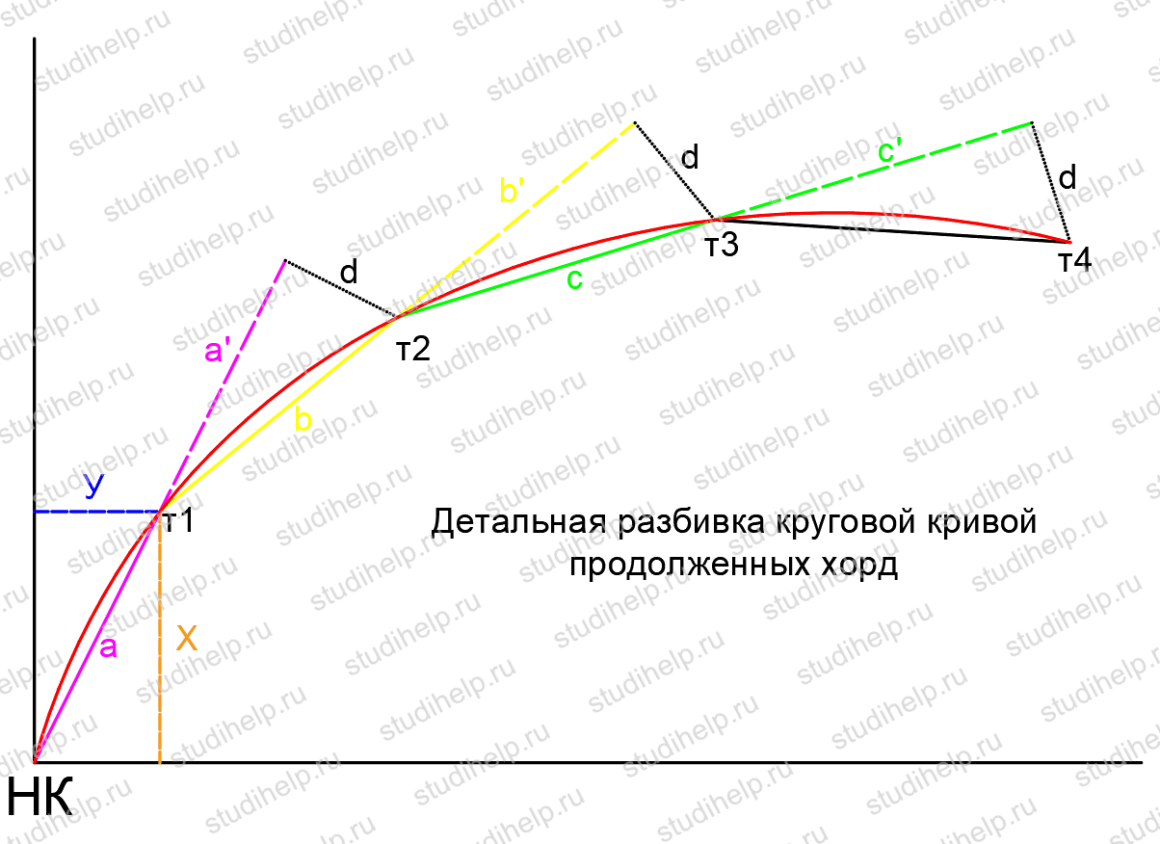
Детальная разбивка круговой кривой способом прямоугольных координат
Наиболее популярный способ. Применяется для равнинной местности. Основное преимущество - положение всех точек кривой определяется независимыми промерами, в итоге погрешности при переходе от одной точки к другой не накапливаются. Ось Х является тангенсом, начало – начало кривой (НК) или её конец (КК), шаг разбивки, d - шаг разбивки (обычно 5м, 10м, 20м).
Координаты точки, расположенной на расстоянии d от начала кривой НК:
хi = R * sin (βi)
yi = R * (1 - cos(βi)
где βi = (Si/R) * (180°/π)